| Jewiki unterstützen. Jewiki, die größte Online-Enzyklopädie zum Judentum.
Helfen Sie Jewiki mit einer kleinen oder auch größeren Spende. Einmalig oder regelmäßig, damit die Zukunft von Jewiki gesichert bleibt ... Vielen Dank für Ihr Engagement! (→ Spendenkonten) |
How to read Jewiki in your desired language · Comment lire Jewiki dans votre langue préférée · Cómo leer Jewiki en su idioma preferido · בשפה הרצויה Jewiki כיצד לקרוא · Как читать Jewiki на предпочитаемом вами языке · كيف تقرأ Jewiki باللغة التي تريدها · Como ler o Jewiki na sua língua preferida |
Sättigungsdampfdruck
Der Sättigungsdampfdruck (auch Gleichgewichtsdampfdruck) eines Stoffes ist der Druck, bei dem der gasförmige Aggregatzustand sich mit dem flüssigen oder festen Aggregatzustand im Gleichgewicht befindet. Der Sättigungsdampfdruck ist von der Temperatur abhängig.
Die Sättigungsdampfdruckkurve (Sättigungsdampfdrucklinie, Dampfdruckkurve, Dampfdrucklinie) beschreibt den Sättigungsdampfdruck in Abhängigkeit von der Temperatur. Sie entspricht der Phasengrenzlinie der gasförmigen Phase im Phasendiagramm.
Achtung: In der Chemie wird üblicherweise der Sättigungsdampfdruck mit „Dampfdruck“ abgekürzt. Hier ist die Gefahr groß, dass man den Begriff des Sättigungsdampfdruckes mit dem des Partialdrucks verwechselt. Deshalb wird der Begriff „Dampfdruck“ hier nicht verwendet.
Geschichte
Im 19. Jahrhundert beschäftigte sich John Dalton mit der Frage, wie viel Wasserdampfvolumen notwendig war, um die Luft zur Sättigung zu bringen. Seine erste Feststellung war, dass dieses Volumen sehr stark von der Temperatur abhängt.
Definition
Der Sättigungsdampfdruck eines Reinstoffes im flüssigen oder festen Aggregatzustand bei gegebener Temperatur ist der Druck, der im thermodynamischen Gleichgewicht in einer ansonsten leeren Kammer über der flüssigen bzw. festen Phase entsteht. In diesem Zustand bestehen beide Phasen stabil nebeneinander, keine wächst auf Kosten der anderen, denn die Verdampfung der Flüssigkeit bzw. Sublimation des Feststoffes ist mengenmäßig gleich der Kondensation bzw. Resublimation des Gases. Bei einer Temperatur- oder Volumenänderung verdampft oder kondensiert so viel des Stoffes, bis im Gleichgewicht wieder der Sättigungsdampfdruck erreicht ist.
Bei Temperaturen oberhalb des Tripelpunkts entsteht bei Kondensation die flüssige Phase, unterhalb des Tripelpunkts der Feststoff, zum Beispiel Iod bei Raumtemperatur.
Befinden sich im ansonsten leeren Probenvolumen mehrere ineinander unlösliche flüssige Phasen, so entsteht darüber ein Gesamtdruck in Höhe der Summe der Sättigungsdampfdrucke der einzelnen Stoffe. Ist nach Erhitzung oder Expansion für eine der Komponenten der Sättigungsdampfdruck höher als der Gesamtdruck, so beginnt diese Komponente zu sieden.
Eine Lösung aus mehreren Komponenten besitzt einen Sättigungsdampfdruck, der außer von der Temperatur auch von der Zusammensetzung der Lösung abhängig ist. Jede Komponente trägt mit einem Partialdruck bei, der sich von ihrem eigenen Sättigungsdampfdruck unterscheiden kann. Die Zusammensetzung des Dampfes hängt von der Temperatur ab und stimmt im Allgemeinen nicht mit der Zusammensetzung der Lösung überein.
Formelzeichen und Einheit
Für den Sättigungsdampfdruck wird meist das Formelzeichen E verwandt, es sind jedoch auch weitere Formen wie es und ps, max, für flüssiges Wasser speziell ew und pw, max sowie für Eis ei und pi, max gebräuchlich. Die jeweiligen Indizes finden sich auch beim groß geschriebenen E. Je nach Anwendungsgebiet werden unterschiedliche Druckeinheiten genutzt, wobei in den Naturwissenschaften Hektopascal (hPa) und Megapascal (MPa), in den Ingenieurswissenschaften hingegen Bar (bar) am gebräuchlichsten sind.
Der Sättigungsdampfdruck im Phasendiagramm
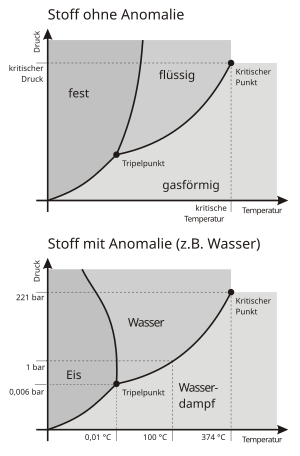
Im Phasendiagramm ist der Sättigungsdampfdruck der Wert des Druckes entlang der hier als schwarz gekennzeichneten Phasengrenzlinie zwischen der Gasphase und der korrespondierenden festen bzw. flüssigen Phase. Diese Phasengrenzlinie wird daher auch als Dampfdruckkurve oder Sättigungsdampfdruckkurve bezeichnet. Für das Phasengleichgewicht von Gas-Festkörper heißt der Sättigungsdampfdruck auch Sublimationsdruck und für das Phasengleichgewicht von Gas-Flüssigkeit auch Siededruck. Zu beachten ist hierbei, dass bei Temperaturen über dem kritischen Punkt keine flüssige Phase und somit auch kein Sättigungsdampfdruck mehr existieren. Des Weiteren spielt die Phasengrenzlinie zwischen Feststoff und Flüssigkeit, die so genannte Schmelzkurve, keine Rolle für den Sättigungsdampfdruck.
Anwendungen und Bedeutung
Der Sättigungsdampfdruck ist ein Maß für den Anteil derjenigen Moleküle oder Atome, die genügend Energie besitzen, die Nah- und Fernordnung (die Kohäsionskräfte und die Oberflächenspannung), zu überwinden und in die gasförmige Phase zu wechseln. Die Wahrscheinlichkeit dafür gibt die Boltzmann-Statistik an. Daher ist die Dampfdruckkurve proportional zum Boltzmann-Faktor:
wobei die Verdampfungsenergie eines Moleküls oder Atoms ist.
Daraus ergibt sich, dass im Gleichgewichtszustand die Teilchenzahl eines spezifischen Gasvolumens bei höheren Temperaturen größer als bei niedrigeren Temperaturen ist, was gleichbedeutend damit ist, dass mit der Temperatur die Teilchendichte ansteigt.
Wichtige Beispiele sind Wasserdampf und Luftfeuchtigkeit. Viele Feuchtemaße werden über Dampfdruck und Sättigungsdampfdruck definiert oder berechnet, besonders im Zusammenhang der relativen Luftfeuchtigkeit, des Sättigungsdefizits und des Taupunkts.
Ein Beispiel für eine Anwendung des Sättigungsdampfdruckes in der Technik ist die Gefriertrocknung, ein weiteres die Druckkochung (siehe Schnellkochtopf). In der Bauphysik wird nach dem Glaser-Verfahren (einem Vergleich von Sattdampfdrücken entsprechend dem Temperaturprofil und den jeweils theoretisch herrschenden Partialdampfdrücken an den Schichtgrenzen des Bauteils) stationär abgeschätzt, ob ein vorgesehenes Bauteil durch ausfallendes Tauwasser gefährdet ist.
Berechnung und Einflussfaktoren
Für die Berechnung des Sättigungsdampfdruckes kann man die Clapeyron-Gleichung bzw. speziell für den Phasenübergang flüssig nach gasförmig auch die Clausius-Clapeyron-Gleichung nutzen. In Anwendung auf den Sättigungsdampfdruck lautet diese:
Die einzelnen Formelzeichen stehen für folgende Größen:
- Es – Sättigungsdampfdruck
- qv – spezifische Verdampfungswärme (Verdampfungswärme pro Masse)
- Rw – spezifische Gaskonstante
- T – Temperatur
Diese Gleichung ist jedoch mit praktischen Problemen behaftet, da man sie nur schlecht integrieren kann (Temperaturabhängigkeit der Verdampfungswärme). Wenn man annimmt, dass (die Verdampfungswärme) konstant wäre dann ergibt sich für den Sättigungsdampfdruck:
Im Falle des für viele Anwendungen sehr wichtigen Sättigungsdampfdruckes des Wassers hat man daher verschiedene Näherungsgleichungen entwickelt, deren einfachster Typ die Magnus-Formeln sind. Die derzeit exakteste Gleichung zur Berechnung des Dampfdruckes über Wasser ist die Goff-Gratch-Gleichung – ein Polynom sechsten Grades in Logarithmen der Temperatur – die auch von der Weltorganisation für Meteorologie empfohlen wird. Ungenauer ist die in VDI/VDE 3514 Blatt 1 angeführte Formel.[1]
Berechnung des Sättigungsdampfdrucks von Wasser über die Magnus-Formel
Der Sättigungsdampfdruck für Wasserdampf kann mit Hilfe der Magnus-Formel (hier die international anerkannte Formel nach Sonntag 1990, siehe Literatur) berechnet werden.[1]
Über ebenen Wasseroberflächen
Über ebenen Eisoberflächen
Hinweise
 Wikibooks: Datentabelle mit genaueren Formeln – Lern- und Lehrmaterialien
Wikibooks: Datentabelle mit genaueren Formeln – Lern- und Lehrmaterialien
In den Magnus-Formeln ist zu beachten, dass für t die Temperatur in Grad Celsius und nicht in Kelvin einzutragen ist. Der sich ergebende Sättigungsdampfdruck hat die Einheit des Vorfaktors , also bei dem hier angegebenen Werten hPa. Jenseits von auf der Erde natürlich auftretenden Temperaturwerten kann die Abweichung der empirisch ermittelten Magnus-Formel zum realen Wert stark zunehmen, weshalb man sich auf die angegebenen Temperaturbereiche beschränken sollte.
Die Magnus-Formeln gelten nur für ebene Oberflächen und auch hier nur für reines Wasser. Ihr Fehler ist jedoch vergleichsweise recht groß, so dass diese beiden Effekte bei einer geringen Ausprägung meist vernachlässigbar sind. Die Standardabweichung der Ergebnisse beträgt beidseitig bis zu einem halben Prozent. Bei gekrümmten Oberflächen, beispielsweise bei kugelförmigen Tröpfchen, ist der Sättigungsdampfdruck höher (Krümmungseffekt siehe unten), hingegen bei salzhaltigen Lösungen geringer (Lösungseffekt siehe unten). Diese beiden modifizierenden Einflüsse spielen eine wesentliche Rolle bei der Bildung von Niederschlagsteilchen.
Im Laborexperiment kann Kondensation über einer ebenen Fläche mit destilliertem Wasser und einer sehr reinen Luft erst nach Übersättigungen von mehreren hundert Prozent erreicht werden. In der realen Atmosphäre spielen hingegen Aerosole eine wesentliche Rolle als Kondensationskeime. Dies hat zur Folge, dass man in der Realität selten Übersättigungen von mehr als einem Prozent beobachtet.
Zum Vergleich der Magnus-Formel mit einer anderen Darstellungsform ist der Artikel Wasserdampf zu empfehlen. Die Magnus-Formel wurde erstmals 1844 von Heinrich Gustav Magnus aufgestellt und seitdem lediglich durch genauere Werte ergänzt, wobei die hier genutzten Werte aus D. Sonntag (1990) stammen. Eine genauere Berechnung, sowie viele Beispielwerte, finden sich im nächsten Abschnitt.
Effekte
Im Gegensatz zum durch die obigen Gleichungen beschriebenen Idealfall eines Reinstoffes und einer ebenen Oberfläche zeigen sich in der Realität weitere Einflussfaktoren, welche den letztendlichen Sättigungsdampfdruck mitbestimmen.
Krümmungs- und Lösungseffekt
Bei Bildung von Flüssigkeitspartikel an Kondensationskernen tritt der Krümmungseffekt auf. Es zeigt sich dabei, dass über den gekrümmten Oberflächen der entstehenden Flüssigkeitstropfen ein höherer Sättigungsdampfdruck auftritt, als im Vergleich zu einer planaren Wasseroberfläche. Liegt die Flüssigkeit bei einer Änderung des Aggregatzustands nicht als Reinstoff vor, so muss man auch den Lösungseffekt beachten. Die in der Flüssigkeit gelösten Teilchen erschweren es hierbei den Flüssigkeitsverbund zu verlassen, weshalb der Sättigungsdampfdruck niedriger ist, als es bei einer reinen Flüssigkeit der Fall wäre.
Unter atmosphärischen Bedingungen treten beide Effekte meist gemeinsam auf, und eine alleinstehende Betrachtung ist wenig zielführend.
Ladungseffekt
Auch die elektrische Ladung der Oberfläche hat eine Auswirkung auf den Sättigungsdampfdruck, welche jedoch im Vergleich zu den anderen Effekten minimal ist und daher keine praktische Rolle spielt.
Korrekturfaktoren für feuchte Luft
Die Korrekturfaktoren (engl.: enhancement factor) sind nötig, da der Wasserdampf nicht in reiner Form vorliegt, sondern innerhalb der feuchten Luft. Sie gelten lediglich bei einem Luftdruck von 1013,25 hPa (Normaldruck). Bei höheren Drücken sind sie größer und dementsprechend bei niedrigeren Drücken kleiner.
- über Wasser im Temperaturintervall von −50 °C bis 90 °C:
- über Eis im Temperaturintervall von −90 °C bis 0 °C:
Da die Korrekturfaktoren temperaturabhängig sind und in den obigen Werten recht große Temperaturintervalle umfassen, stellen sie nur recht grobe Näherungen an die tatsächliche Abweichung dar. Die negativen Temperaturen über Wasser beziehen sich auf unterkühltes Wasser. Um die resultierenden Werte für den Sättigungsdampfdruck zu erhalten, gilt:
- ( – Tabellenwert)
- ( – Tabellenwert)
Zusammenhang mit der Sättigungsmenge
Nach der allgemeinen Gasgleichung ist der Sättigungsdampfdruck (näherungsweise) auch das Produkt der Sättigungsmenge mit der individuellen Gaskonstante und der Temperatur (in Kelvin). Als Formel etwa so dargestellt:
vgl. Dampfdruck bzw. Sättigung.
- γ steht hier noch für das jeweilige Gas (z. B. Wasserdampf) – mit Gaskonstante Rγ,
- φ für den alternativen Aggregatzustand („Phase“, fest bzw. flüssig); bei γ = Wasserdampf ist Eγ,φ der Wasserdampfdruck und ργ,φ die Sättigungsmenge „über Eis“ bzw. „über Wasser“.
Neben der Bezeichnung Sättigungsmenge findet man auch Sättigungskonzentration und Sättigungs-(dampf-)dichte (Titel von Sonntag 1982), die SI-Einheit ist zumeist g/m3. Bei Wasserdampf spricht man auch von der maximalen Luftfeuchte.
Literatur
- Dietrich Sonntag: Important new Values of the Physical Constants of 1986, Vapour Pressure Formulations based on ITS-90, and Psychrometer Formulae. In: Zeitschrift für Meteorologie. Bd. 40, Nr. 5, 1990, ISSN 0084-5361, S. 340–344.
- Leslie A. Guildner, Daniel P. Johnson, Frank E. Jones: Vapor pressure of Water at Its Triple Point. In: Journal of Research of the National Bureau of Standards. Section A: Physics and Chemistry. Bd. 80A, Nr. 3, 1976, ISSN 0022-4332, S. 505–521, doi:10.6028/jres.080A.054
- Daniel M. Murphy, Thomas Koop: Review of the vapour pressures of ice and supercooled water for atmospheric applications. In: Quarterly Journal of the Royal Meteorological Society. Bd. 131, Nr. 608, 2005, ISSN 0035-9009, S. 1539–1565, doi:10.1256/qj.04.94.

Siehe auch
- Raoultsches Gesetz – Dampfdruckveränderungen in Lösungen
- Siedepunkt
- Tripelpunkt
- Bancroft-Punkt
- Antoine-Gleichung
Weblinks
- Online-Rechner für die wichtigsten meteorologischen Größen
- Gleichungen zum Sättigungsdampfdruck, zusammengestellt von Holger Vömel (engl.)
- Goff-Gratch-Gleichung in der englischsprachigen Wikipedia (engl.)
- Online-Rechner-Luftfeuchte. Errechnet für Temperaturen von −20 °C bis +70 °C u. a. den Sättigungsdampfdruck (Näherungsformeln nach B. Glück)
Fußnoten
| Dieser Artikel basiert ursprünglich auf dem Artikel Sättigungsdampfdruck aus der freien Enzyklopädie Wikipedia und steht unter der Doppellizenz GNU-Lizenz für freie Dokumentation und Creative Commons CC-BY-SA 3.0 Unported. In der Wikipedia ist eine Liste der ursprünglichen Wikipedia-Autoren verfügbar. |














