| Jewiki unterstützen. Jewiki, die größte Online-Enzyklopädie zum Judentum.
Helfen Sie Jewiki mit einer kleinen oder auch größeren Spende. Einmalig oder regelmäßig, damit die Zukunft von Jewiki gesichert bleibt ... Vielen Dank für Ihr Engagement! (→ Spendenkonten) |
How to read Jewiki in your desired language · Comment lire Jewiki dans votre langue préférée · Cómo leer Jewiki en su idioma preferido · בשפה הרצויה Jewiki כיצד לקרוא · Как читать Jewiki на предпочитаемом вами языке · كيف تقرأ Jewiki باللغة التي تريدها · Como ler o Jewiki na sua língua preferida |
Baum (Graphentheorie)
Ein Baum ist in der Graphentheorie ein spezieller Typ von Graph, der zusammenhängend ist und keine geschlossenen Pfade enthält, d. h. damit lässt sich eine Monohierarchie modellieren. Je nachdem, ob die Kanten des Baums eine ausgezeichnete und einheitliche Richtung besitzen, lassen sich graphentheoretische Bäume unterteilen in ungerichtete Bäume und gewurzelte Bäume, und für gewurzelte Bäume in Out-Trees, bei denen die Kanten von der Wurzel ausgehen, und In-Trees, bei denen Kanten in Richtung Wurzel zeigen.
Ein Baum ist ein Wald mit genau einer Zusammenhangskomponente.[1]

Definitionen
Ein Baum ist ein zusammenhängender kreisfreier ungerichteter Graph. Die Knoten mit Grad 1 heißen Blätter, die übrigen Knoten heißen innere Knoten.
Ein gerichteter Baum ist ein gerichteter Graph, der ein ungerichteter Baum ist, wenn man die Richtungen der Kanten ignoriert. Er ist also ein gerichteter schwach zusammenhängender kreisfreier Graph. Bei vielen Autoren müssen die Richtungen einheitlich von einem Knoten weg oder auf einen Knoten zu orientiert sein. Dafür gibt es aber auch den schärferen Begriff des gewurzelten Baums.
Ein gewurzelter Baum ist ein gerichteter von einem Knoten aus stark zusammenhängender kreisfreier Graph. Der den starken Zusammenhang definierende Knoten wird Wurzel genannt. Er hat Eingangsgrad 0 und ist der einzige Knoten mit dieser Eigenschaft. Alle Knoten mit Ausgangsgrad 0 heißen Blätter. Alle Knoten mit positivem Ausgangsgrad heißen innere Knoten. So geht die Definition eines Out-Trees.
Werden die Richtungen aller Kanten eines solchen Graphen invertiert, so wird er zu einem In-Tree. Dieser wird ebenfalls als gewurzelter Baum angesehen.
Man kann jeden ungerichteten Baum an einem beliebigen Knoten fassen und „schütteln“ – die Schwerkraft gibt allen Kanten eine definierte Richtung von weg, die aus dem ursprünglich ungerichteten Baum einen gewurzelten machen mit als Wurzel.
Den Kanten eines ungerichteten Baums kann man verschiedene Richtungen geben und so gerichtete Bäume ableiten. Genau davon sind Out-Trees und ebenso viele sind In-Trees. Entfernt man umgekehrt bei einem gerichteten Baum die Orientierung der Kanten, so erhält man einen ungerichteten Baum.
Eigenschaften
Ein endlicher Graph mit Knoten und Kanten kann durch folgende äquivalente Aussagen als Baum definiert werden:
- Zwischen je zwei Knoten von gibt es genau einen Pfad.
- ist zusammenhängend und enthält keinen Kreis
- ist leer oder ist zusammenhängend und es gilt .
- ist leer oder enthält keinen Kreis und es gilt .
- ist minimal zusammenhängend, das heißt ist zusammenhängend, aber nicht mehr zusammenhängend, sobald man eine beliebige Kante daraus entfernt.
- ist maximal azyklisch, das heißt ist kreisfrei, aber jede weitere Kante zwischen zwei beliebigen Knoten erzeugt einen Kreis.
Im Falle unendlicher Graphen müssen hier die dritte und vierte Bedingung aus der Äquivalenz ausgenommen werden.
Beweise
Zwischen je zwei Knoten von gibt es mindestens einen Pfad, weil jeder Baum zusammenhängend ist. Gäbe es zwei Knoten von mit mindestens zwei Pfaden, dann gäbe es zwei Knoten und auf diesen Pfaden, deren Pfade keinen gemeinsamen inneren Knoten haben (disjunkte Wege), zum Beispiel und . Dann wäre ein Kreis von im Widerspruch zur Annahme, dass ein Baum ist.
- ist leer oder ist zusammenhängend und es gilt .
Dies lässt sich mit vollständiger Induktion zeigen. Für , also einen leeren Graphen mit einem einzelnen Knoten und ohne Kanten, gilt . Nach Induktionsvoraussetzung nehmen wir an, dass die Gleichung für jeden Baum mit Knoten gilt. Ist ein Graph mit Knoten und die Knoten eines längsten Pfades von . Alle Nachbarn von liegen auf diesem Pfad, sonst wäre er nicht der längste Pfad. ist der einzige Nachbar von , denn sonst würde einen Kreis enthalten. Entfernen wir und die Kante aus , dann erhalten wir einen zusammenhängenden Graphen, denn ist der einzige Nachbar von . Der entstandene Graph hat genau einen Knoten und eine Kante weniger als , also Knoten. Nach Induktionsvoraussetzung gilt , also hat der entstandene Graph Kanten. Daraus folgt, dass der Graph genau Knoten und Kanten hat.
- ist minimal zusammenhängend, das heißt ist zusammenhängend, aber nicht mehr zusammenhängend, sobald man eine beliebige Kante daraus entfernt.
Wäre nach Entfernen der Kante immer noch zusammenhängend, dann würde der entstandene Graph einen Pfad von nach enthalten und wäre ein Kreis von .
- ist maximal azyklisch, das heißt ist kreisfrei, aber jede weitere Kante zwischen zwei beliebigen Knoten erzeugt einen Kreis.
Wäre nach Hinzufügen der Kante immer noch kreisfrei, dann würde keinen Pfad von nach enthalten und wäre nicht zusammenhängend im Widerspruch zur Annahme, dass ein Baum ist.
Weitere Eigenschaften
- Durch Entfernen einer Kante zerfällt ein Baum in zwei Teilbäume und bildet damit einen Wald mit zwei Komponenten.
- Entfernt man einen Knoten zusammen mit den anliegenden Kanten, zerfällt ein Baum in einen Wald aus Bäumen, mit als Grad des entfernten Knotens[2]. Entfernt man von einem Baum ein Blatt (), so ist der Rest immer noch ein Baum.[1]
- Durch Hinzufügen einer Kante zwischen zwei vorhandenen Knoten entsteht im ungerichteten Baum ein Kreis.[3]
- Bäume sind aufgrund der Kreisfreiheit stets auch bipartit und können topologisch sortiert werden.
- Bäume sind planar.
Spezielle Bäume
Es existiert eine Vielzahl von Begriffen, die Bäume näher spezifizieren. So gibt es zum Beispiel
- den leeren Graph. Dieser enthält keine Knoten und Kanten.
- den isolierten Knoten ohne Kanten
- lineare Graphen . Die inneren Knoten haben jeweils genau zwei Nachbarn.
- Sterngraphen oder . Diese enthalten einen inneren Knoten und Blätter.
- Raupenbäume. Alle Blätter haben einen maximalen Abstand von 1 zu einem zentralen Pfad.
- Bäume mit konstantem Verzweigungsfaktor, also Grad der inneren Knoten (Bereichsbaum):
- Binärbäume (untergliedern eindimensionale Daten, innere Knoten haben zwei Nachfolger), darunter vollständige Binärbäume, AVL-Baum und Rot-Schwarz-Baum,
- Quadtrees (untergliedern zweidimensionale Daten, innere Knoten haben vier Nachfolger),
- Octrees (untergliedern dreidimensionale Daten, innere Knoten haben acht Nachfolger),
- Binomial-Bäume haben einen variablen, aber festgelegten Verzweigungsfaktor. Ein Binomial-Baum der Ordnung k besitzt eine Wurzel mit Grad k, deren Kinder genau die Ordnung besitzen.
- Bäume können nach ihrer Höhe, dem Gewicht der Knoten oder der Anordnung der Wurzel balanciert sein.
Binärbaum mit Knotentypen
balancierter Binärbaum
Binomial-Heap mit 13 Elementen. Die Schlüssel der Väter sind höchstens so groß wie die Schlüssel ihrer Kinder.
Die Sterngraphen , , und
Zeichnen von Bäumen
Die grafische Ausgabe eines Baums ist ein nicht triviales Problem. Allgemein gilt, dass jeder Baum planar, das heißt ohne Überschneidungen der Kanten gezeichnet werden kann. Je nach Anwendungszweck gibt es weitere Wünsche an die Art der Ausgabe:
- alle Kanten sind gerade Linien
- alle Knoten haben ganzzahlige Koordinaten
- möglichst kleiner Platzbedarf bei möglichst ästhetischem Ergebnis
- alle Kanten vom Elternelement zum Kind streng monoton fallend
Es gibt verschiedene Algorithmen, deren Ergebnisse recht verschieden aussehen. Meist lösen sie nur einige, aber nicht alle Wünsche an die Ausgabe. Bekannte Algorithmen sind die HV-Bäume und der Algorithmus von Walker.
Anzahl von Bäumen
Es gibt verschiedene bezeichnete Bäume mit Knoten. Diese Aussage ist als Cayley-Formel bekannt. Einen einfachen Beweis liefert der Prüfer-Code, der eine Bijektion zwischen allen möglichen Codes der Länge und allen bezeichneten Bäumen auf Knoten ermöglicht.
Spannbäume
Jeder ungerichtete, zusammenhängende Graph enthält einen ihn aufspannenden Baum als Teilgraphen. Minimale Spannbäume haben eine möglichst kleine Anzahl von Kanten oder eine möglichst kleine Summe der Kantengewichte. Die Berechnung minimaler Spannbäume findet direkte Anwendung in der Praxis, beispielsweise für die Erstellung von kostengünstigen zusammenhängenden Netzwerken, wie beispielsweise Telefonnetze oder elektrische Netze.
Verallgemeinerungen
Wald
Ein Wald ist ein ungerichteter Graph, dessen Zusammenhangskomponenten Bäume sind.
k-Baum
Ein ungerichteter Graph heißt -Baum, wenn er wie folgt rekursiv erzeugbar ist:
- Der vollständige Graph ist ein -Baum.
- Fügt man zu einem -Baum einen neuen Knoten hinzu, indem man mit allen Knoten einer Clique der Größe aus verbindet, so ist dieser neue Graph ebenfalls ein -Baum.
Ein partieller -Baum entsteht durch die Entfernung von Kanten aus einem -Baum: Ist ein -Baum, so ist mit ein partieller -Baum.[4][5][6][7]
Durch die angegebene Definition haben partielle k-Bäume immer mindestens k Knoten, was nicht immer wünschenswert ist. Darum gibt es auch die folgende Definition:
Eine weitere Eigenschaft ist, dass die Menge der partiellen k-Bäume gleich der Menge der Graphen mit Baumweite höchstens k ist.[11][12]
Siehe auch
Anmerkungen
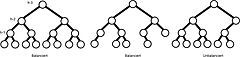
- ↑ Einige der dargestellten Bäume sind isomorph zueinander; nämlich beide Bäume in Fig. 2 sowie in Fig. 3 (von links gezählt) die Bäume 1 und 3 sowie 2 und 4. Es sind nur ungerichtete Bäume dargestellt. Fasst man den obersten Knoten als Wurzel auf, so ergeben sich entsprechend unterschiedliche (heteromorphe) gewurzelte Bäume.
Literatur
- Frank Gurski, Irene Rothe, Jörg Rothe, Egon Wanke: Exakte Algorithmen für schwere Graphenprobleme. Springer-Verlag, Berlin/ Heidelberg 2010, ISBN 978-3-642-04499-1.
- Sven Krumke, Hartmut Noltemeier: Graphentheoretische Konzepte und Algorithmen. 3. Auflage. Springer Vieweg Verlag, Wiesbaden 2012, ISBN 978-3-8348-1849-2.
Weblinks
Einzelnachweise
- ↑ 1,0 1,1 Reinhard Diestel: Graphentheorie. 3., neu bearb. und erw. Auflage. Springer, Berlin 2006, ISBN 3-540-21391-0, S. 14.
- ↑ Angelika Steger: Diskrete Strukturen. 2 Auflage. Band 1: Kombinatorik, Graphentheorie, Algebra, Springer, Berlin 2007, ISBN 978-3-540-46660-4, S. 65.
- ↑ Stephan Hußmann, Brigitte Lutz-Westphal: Kombinatorische Optimierung erleben : in Studium und Unterricht. 1 Auflage. Vieweg, Wiesbaden 2007, ISBN 978-3-528-03216-6, S. 47.
- ↑ Frank Gurski, Irene Rothe, Jörg Rothe, Egon Wanke: Exakte Algorithmen für schwere Graphenprobleme. Springer-Verlag, Berlin/ Heidelberg 2010, ISBN 978-3-642-04499-1.
- ↑ Sven Krumke, Hartmut Noltemeier: Graphentheoretische Konzepte und Algorithmen. Vieweg+Teubner Verlag, 2012, ISBN 978-3-8348-2264-2.
- ↑ Daniel Granot: On some optimization problems on k-trees and partial k-trees. In: Discrete Applied Mathematics. Elsevier, 1994.
- ↑ Janka Chlebı́ková: Partial k-trees with maximum chromatic number. In: Discrete Applied Mathematics. 2002
- ↑ Xiao Zhou, Shin-ichi Nakano, Takao Nishizeki: Edge-Coloring Partial k-Trees. In: Journal of Algorithms. Nr. 21, 1996 S. 598-617.
- ↑ Ton Kloks: Treewidth. Springer-Verlag, Berlin/ Heidelberg 1994, ISBN 3-540-48672-0.
- ↑ A. Yamaguchi, H. Mamitsuka: Finding the Maximum Common Subgraph of a Partial k-Tree and a Graph with a Polynomially Bounded Number of Spanning Trees. Springer, Berlin/ Heidelberg 2003, ISBN 3-540-24587-1.
- ↑ Hans L. Bodlaender: A partial k-arboretum of graphs with bounded treewidth. In: Theoretical Computer Science. 1998 S. 1-45.
- ↑ Jan van Leeuwen: Algorithms and Complexity Theory. In: Handbook of Theoretical Computer Science. vol. A, North Holland, Amsterdam 1990, S. 527-631.
| Dieser Artikel basiert ursprünglich auf dem Artikel Baum (Graphentheorie) aus der freien Enzyklopädie Wikipedia und steht unter der Doppellizenz GNU-Lizenz für freie Dokumentation und Creative Commons CC-BY-SA 3.0 Unported. In der Wikipedia ist eine Liste der ursprünglichen Wikipedia-Autoren verfügbar. |